Simple Password Exponential Key Exchange

Simple Password Exponential Key Exchange(SPEKE) is based on Diffie-Hellman Key Exchange(DH), which is a balanced PAKE protocol. The difference of SPEKE against DH is that its group generator is derived from the password rather than a public assumption. Only who knows the password can produce this private generator.

How it work

The SPEKE has two stages:

1. Session key establishment by DH
2. Authentication

Although there are some variations of SPEKE, their stage 1 is basically same. It uses the DH protocol to build a session key.

The stage 2 is to authenticate the conversation subject. We will introduce two ways to authenticate in this content.

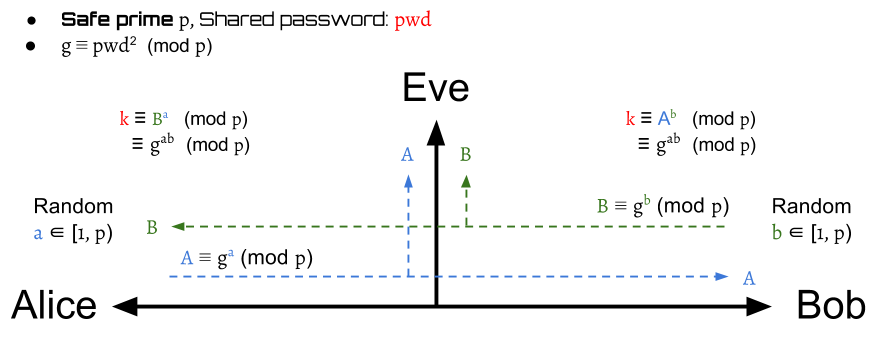
Stage 1: Session Key Establishment

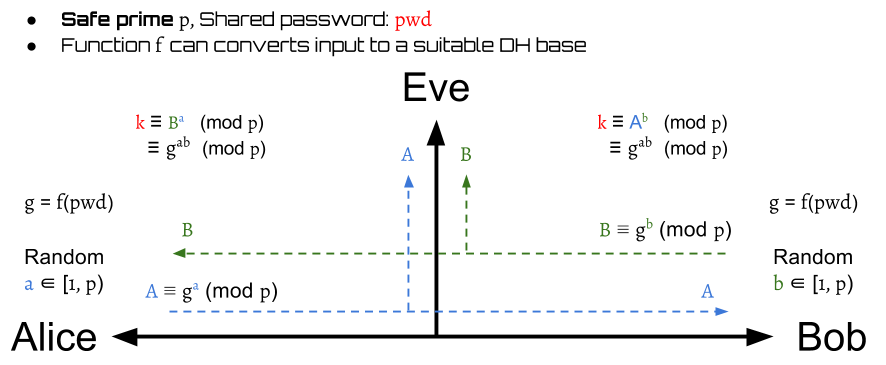
The stage 1 of SPEKE is shown above. Instead of using a public group generator directly, SPEKE has a function $f$ that can produce generators by inputs. Thus, we use the shared password $pwd$ to create a generator $g = f(pwd)$ and use it to complete the DH protocol.

The modulo $p$ used here is a safe prime \begin{aligned} p = 2q + 1 \ \text{, where $q$ is also a prime} \end{aligned}

After this stage finishes, the Alice and Bob can get a symmetric session key $k$ to encrypt/decrypt the transmitted messages.

Stage 2 with Challenge–Response Authentication

Challenge–Response Authentication is one way to verify whether or not the other party is Bob. The detail can be seen in the following terms.

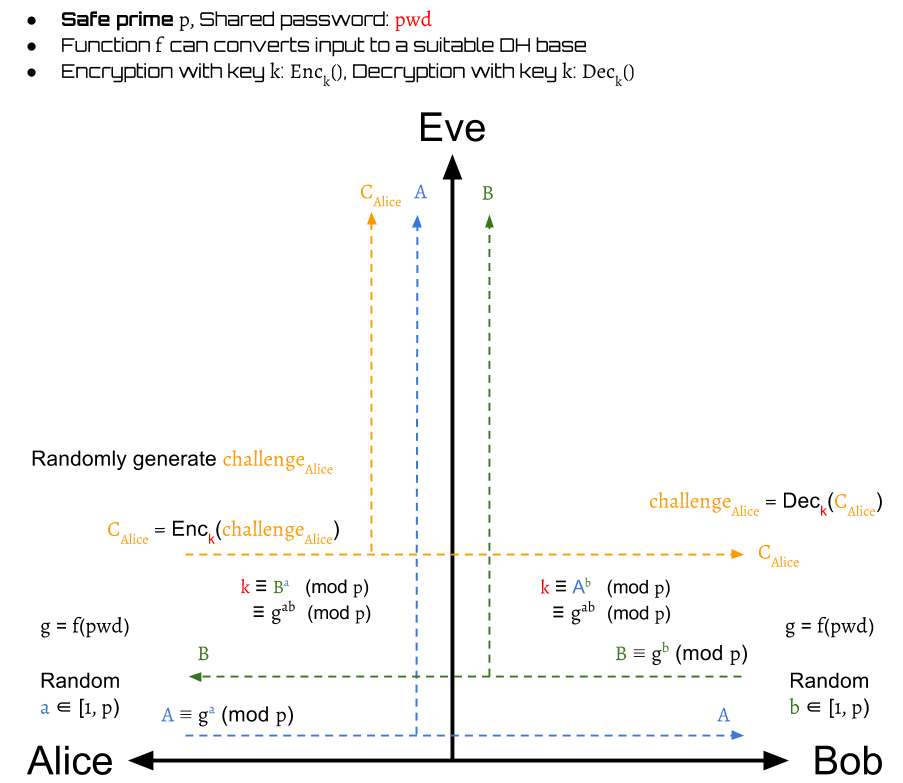Alice generates a random challenge $challenge_{Alice}$ and then encrypt it to $C_{Alice}$ by the session key $k$: $C_{Alice} = Enc_k(challenge_{Alice})$

Bob then can decrypt $C_{Alice}$ to $challenge^{Bob}_{Alice}$ by the session key $k$: $challenge^{Bob}_{Alice} = Dec_k(C_{Alice})$

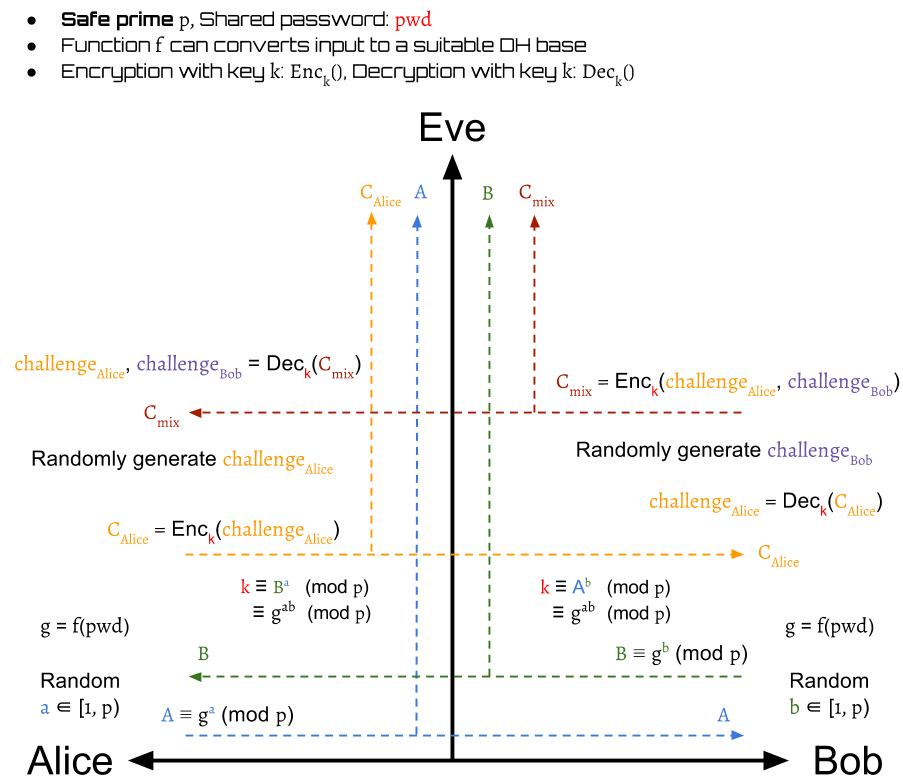Then, Bob also generates a random challenge $challenge_{Bob}$. It is encrypted with $challenge^{Bob}_{Alice}$ into $C_{mix}$ by $k$ and then send back to Alice. $C_{mix} = Enc_k(challenge^{Bob}_{Alice}, challenge_{Bob})$

After Alice receives $C_{mix}$, she can decrypt it to get $challenge^{Bob}_{Alice}, challenge^{Alice}_{Bob} = Dec_k(C_{mix})$

Alice now is able to verify whether or not Bob is valid by comparing the received Bob's decrypted value of her challenge and her original one. $valid(Bob) = \begin{cases} true, & \text{if } challenge^{Bob}_{Alice} = challenge_{Alice} \\[2ex] false, & \text{otherwise} \end{cases}$

If Bob is invalid, then Alice immediately drops the session. Otherwise, the protocol should continue.

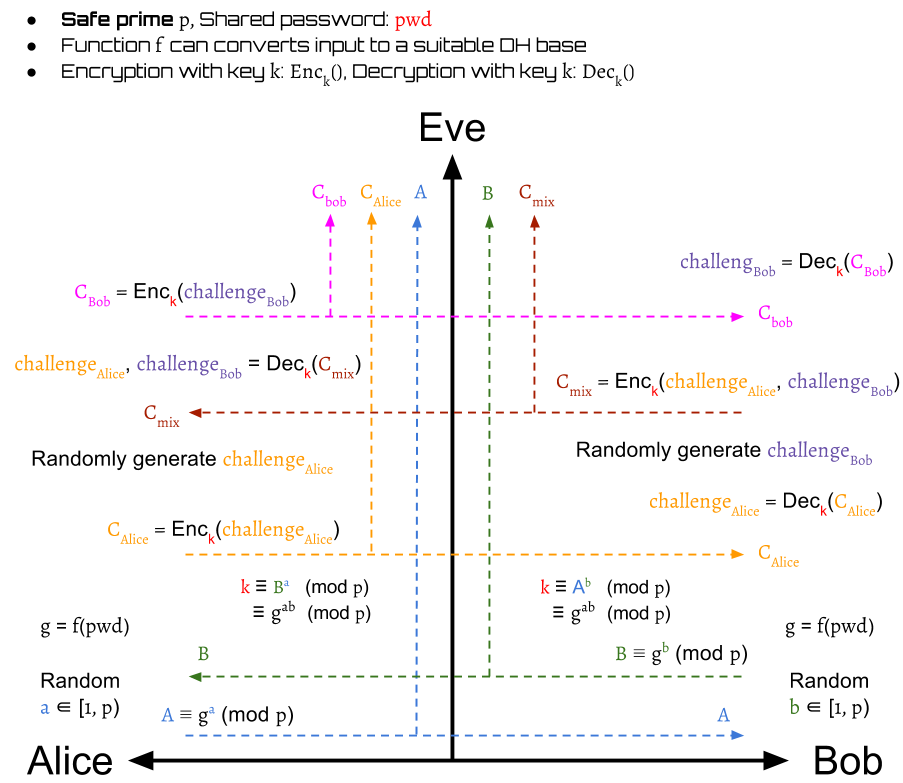
Beside the $challenge^{Bob}_{Alice}$, Alice also get a decrypted value of Bob's challenge $challenge^{Alice}_{Bob}$. This is used as a proof that Alice has the same key $k$ as Bob. Alice sends $C_{Bob}$ to Bob for authentication: $C_{Bob} = Enc_k(challenge^{Alice}_{Bob})$

When Bob receives the $C_{Bob}$, he can decrypt it: $challenge^{Alice}_{Bob} = Dec_k(C_{Bob})$ to compare Alice's decrypted value of his own challenge with his original one.

$valid(Alice) = \begin{cases} true, & \text{if } challenge^{Alice}_{Bob} = challenge_{Bob} \\[2ex] false, & \text{otherwise} \end{cases}$ If they are different, the Bob immediately drops the session. Otherwise, Alice is authenticated and the protocol finishes.

Stage 2 with Hash-Key Authentication

Instead of random challenge, another simpler method to authenticate the other party is to use hash function. The steps consists of the following:

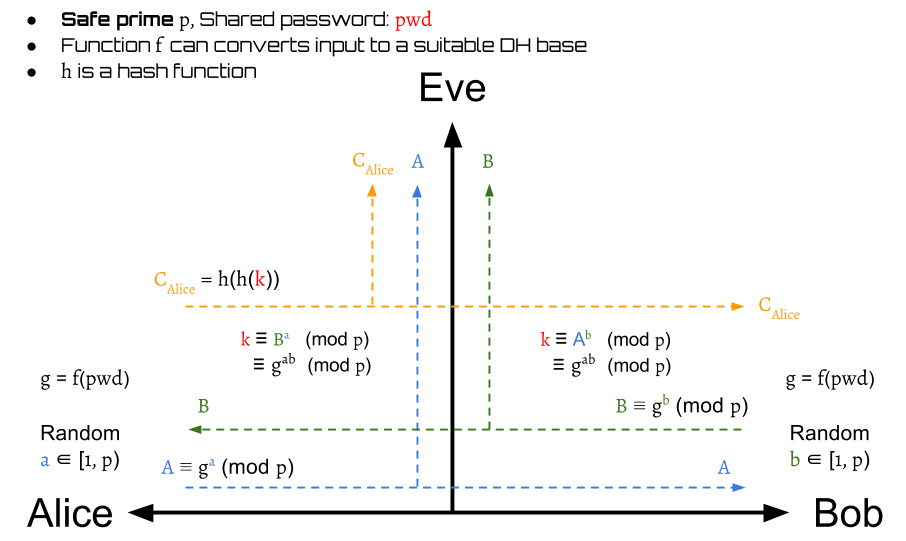First, Alice send twice hashed value of the session key to Bob: $C_{Alice} = h(h(k))$

Then Bob can authenticate Alice by $valid(Alice) = \begin{cases} true, & \text{if } C_{Alice} = h(h(k)) \\[2ex] false, & \text{otherwise} \end{cases}$

If Alice is a invalid party, then the session is dropped. Otherwise, the protocol continues.

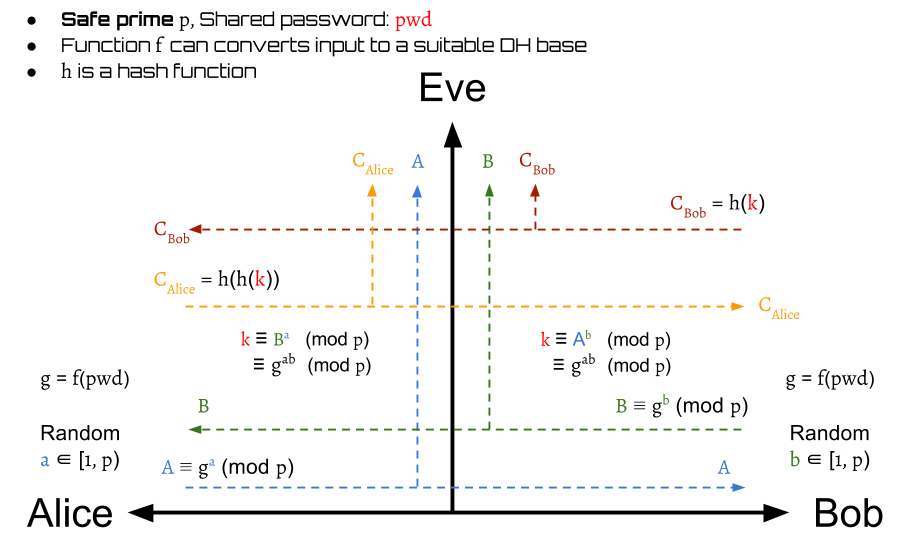
After verifying Alice, Bob also need to prove his identification to Alice. Bob sends
$C_{Bob} = h(k)$ to Alice.

Alice then can certify Bob by $valid(Bob) = \begin{cases} true, & \text{if }h(C_{Bob}) = C_{Alice} \\[2ex] false, & \text{otherwise} \end{cases}$

Finally, they can authenticate mutually.

Summary

Security Issues

Short Exponents

Similar to the case of DH-EKE, partial bits may be predictable.

Test multiple passwords in one time

f(x) = x² mod p

The basic idea to get the generator is to define $f(x) = x^2 \bmod p$, , where $p$ is a safe prime such that $p = 2q + 1$, $q$ is also a prime. Then, the generator $g$ will be computed by $pwd^2 \bmod p$. This makes sure that every $f(x)$ will be a generator of a cyclic subgroup of $G$, where $G = \{ x \vert 0 < x < p \cap x \in N \}$ (We need a proof here!)

If we take $q = 11$ to get a safe prime $p = 23$, then the generators are:

From the table above, one obvious fact is that the attacker is allowed to test two $pwd$ by guessing one $g = f(pwd)$. For example, the attacker can guess the $g = 16 = f(pwd)$. If he doesn't hit, then he knows that $pwd$ is not 4 and 19. In the worst case that the $pwd$ is fixed, the attacker can use half time to force brute the $pwd$.

The collision is guaranteed because \begin{aligned} (q + k + 1)^2 \equiv (q - k)^2 \pmod p \ \text{ ,where $k \in Z, p = 2q + 1$.} \end{aligned}

Proof: $\begin{aligned} (q + k + 1)^2 &\equiv (q + (k + 1))^2 \equiv q^2 + 2q(k+1) + (k+1)^2 \pmod {2q + 1} \\ &\equiv q^2 + 2kq + 2q + k^2 + 2k + 1 \pmod {2q + 1} \\ &\equiv q^2 - 2kq + k^2 + 4kq + 2k + 2q + 1 \pmod {2q + 1} \\ &\equiv (q - k)^2 + 2k(2q + 1) + (2q + 1) \pmod {2q + 1} \\ &\equiv (q - k)^2 + (2k + 1)(2q + 1) \pmod {2q + 1} \\ &\equiv (q - k)^2 \pmod {2q + 1} \end{aligned}$

When $k = 0$, then $(12)^2 \equiv (11)^2 \pmod {23}$. When $k = 1$, then $(13)^2 \equiv (10)^2 \pmod {23}$. ...

f(x) = (hash(x))² mod p

Suppose we have a hash table

Even we use the hash the map the $pwd$ before squaring it, the fact that the attacker is allowed to test two $pwd$ by guessing one $g = f(pwd)$ won't be changed. For example, the attacker guesses $g = 16 = f(pwd)$. If he doesn't hit, then he knows that $pwd$ is not 12 and 13.

Impersonation Attack

The author of J-PAKE points out a two attacks against SPEKE. The first attack allows an attacker to successfully build two sessions with a same victim without knowing the password.

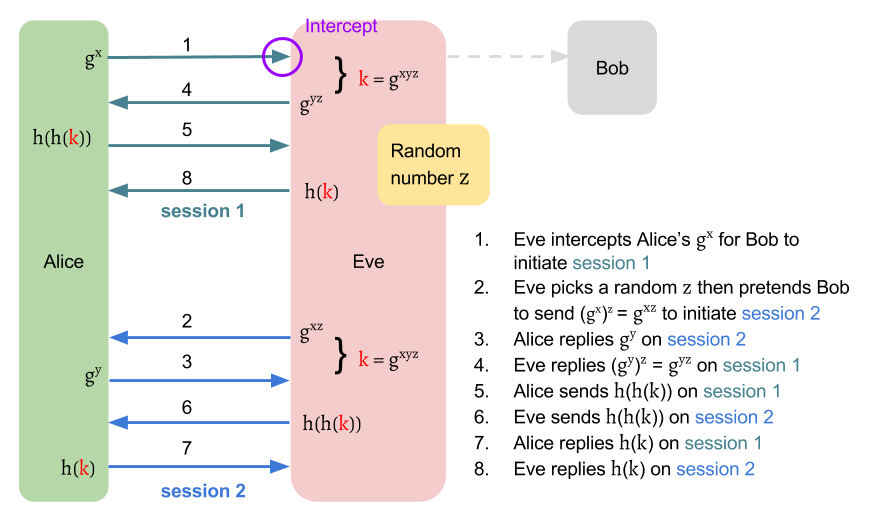
Although the attacker may not get the session key $k$, it's still dangerous. Assume that Alice is a server of a bank. Suppose Alice sends a encrypted message "Pay Jimmy one million" to Bob on session 1. Eve can simply reply this message to Alice on session 2. Since Eve is a valid user who is authenticated as Bob, Alice may follow the received instruction and pay Jimmy one million.

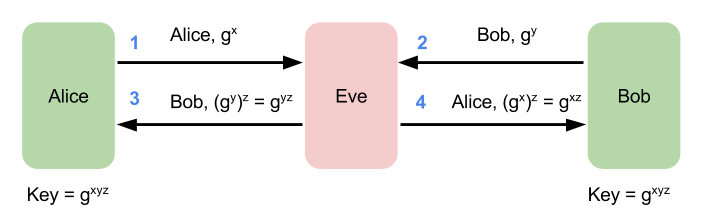
Key-malleability Attack

The author of J-PAKE points out a two attacks against SPEKE. The second attack allows an attacker to have a hand in the session key between two parties without being detected.

Program to verify the generator

We can write a python program like speke.py to verify the generator $g = f(pwd)$ is a generator of a subgroup of $G$.

If $p = 23, f(x) = x^2 \bmod p$, then the output will be as follows:

References

• Strong Password-Only Authenticated Key Exchange
• Simple password exponential key exchange
• Wiki: SPEKE (cryptography)