Hash
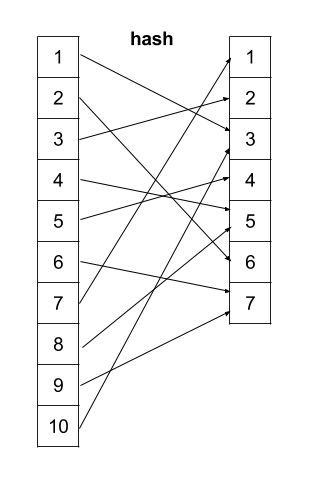 A well-designed hash should not collision when the size of domain space
is same as the size of range(like the figure above, there is no collision
when ).
A well-designed hash should not collision when the size of domain space
is same as the size of range(like the figure above, there is no collision
when ).
| Num/Rnd | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 3 | 2 | 6 | 7 | 1 | 3 |
| 2 | 6 | 7 | 1 | 3 | 2 | 6 |
| 3 | 2 | 6 | 7 | 1 | 3 | 2 |
| 4 | 5 | 4 | 5 | 4 | 5 | 4 |
| 5 | 4 | 5 | 4 | 5 | 4 | 5 |
| 6 | 7 | 1 | 3 | 2 | 6 | 7 |
| 7 | 1 | 3 | 2 | 6 | 7 | 1 |
| 8 | 5 | 4 | 5 | 4 | 4 | 5 |
| 9 | 7 | 1 | 3 | 2 | 6 | 7 |
| 10 | 3 | 2 | 6 | 7 | 3 | 2 |
There is no collision in each round when the size is available. For example, we can see that are never have collisions. The reason is simple. If we can guarantee there is no collision when size is available, then it means that the results in first round will have no collision and it must be one-to-one from the domain space to the range space. Thus, each number in available size will be one-to-one mapped to a different number. In the same manner, the results after second round will keep no collision. The results from first round must also be one-to-one mapped to different numbers in round 2.
From another view, you can prove it by contradiction. Assume that we can guarantee there is no collision when size is available. If we have a collision in the round, then it means that there is two numbers of round are mapped to a same number in the round. This contradict our assumption for no collision when size is available.
On the other hand, the numbers who is out of the available size (e.g., [8, 10] on above table) must have collisions. In addition, after the first round, they will disappear because no number will be mapped to them(they are out of size!).
The hash function must have a pattern. The bold-faced numbers label their periods. If the number will be mapped to another different number in each round. At the first round, it will have choices. At the second round, it still have choices, but there is one choice will be the initial number. If the initial number is mapped, then the period occurs. Otherwise, if the initial number isn't mapped, then there are choices. Similarly, at the third round, it has at most choices to prevent the period occurs. However, at the round, there is no choice to stop period presented. Therefore, the period must happen.
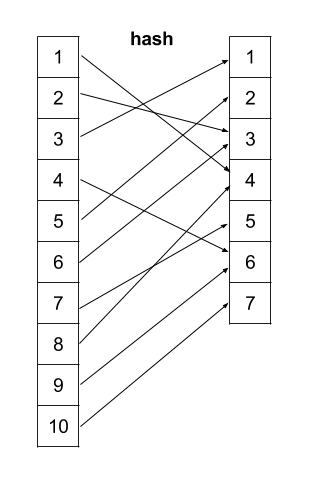
However, if the hash is not well-designed(e.g., collision when ), then ....
| Num/Rnd | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 6 | 3 | 1 | 4 | 6 | 3 | 1 |
| 2 | 3 | 1 | 4 | 6 | 3 | 1 | 4 | 6 |
| 3 | 1 | 4 | 6 | 3 | 1 | 4 | 6 | 3 |
| 4 | 6 | 3 | 1 | 4 | 6 | 3 | 1 | 4 |
| 5 | 2 | 3 | 1 | 4 | 6 | 3 | 1 | 4 |
| 6 | 3 | 1 | 4 | 6 | 3 | 1 | 4 | 6 |
| 7 | 5 | 2 | 3 | 1 | 4 | 6 | 3 | 1 |
| 8 | 4 | 6 | 3 | 1 | 4 | 6 | 3 | 1 |
| 9 | 6 | 3 | 1 | 4 | 6 | 3 | 1 | 4 |
| 10 | 7 | 5 | 2 | 3 | 1 | 4 | 6 | 3 |