Proof of Dijkstra

In this article, the Dijkstra will be proved by mathematical induction. Suppose we have following variables:

• $G$ is the input graph
• $V$ is the set of all vertices
• $K$ is the set containing all visited vertices
• $s$ is source vertex
• $l(x, y)$ is the length of an edge from $x$ to $y$
• $d(x)$ is shortest path distance found by Dijkstra algorithm.

Dijkstra algorithm

$$\begin{align} & \text{Dijkstra($G, s$):} \\ & \space \space \space \space \text{for all $u \in V \space \backslash \space \{ s \} $:} \\ & \space \space \space \space \space \space \space \space d(u) = \infty \\ & \space \space \space \space d(s) = 0 \\ & \space \space \space \space K = \{ \} \\ & \space \space \space \space \text{while $K \neq V$:} \\ & \space \space \space \space \space \space \space \space\text{pick $u \in V - K$ with smallest $d(u)$} \\ & \space \space \space \space \space \space \space \space K = K \cup \{ u \} \\ & \space \space \space \space \space \space \space \space \text{for all vertices $v$ adjacent to $u$:} \\ & \space \space \space \space \space \space \space \space \space \space \space \space \text{if $d(v) > d(u) + l(u, v)$ :} \\ & \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space d(v) = d(u) + l(u, v) \end{align}$$

Proof by mathematical induction

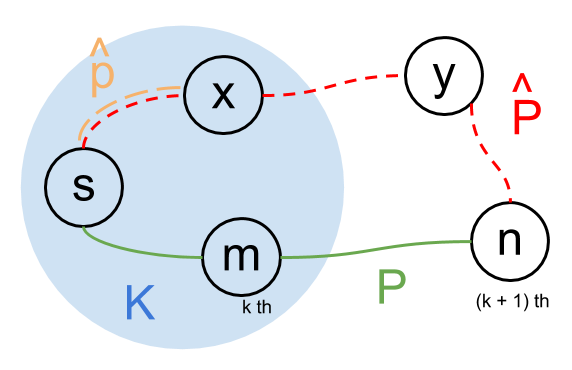
Proof: For each $x \in K, \space d(x)$ is the shortest path from $s$ to $x$.

1. Basis: when $\vert K \vert = 1, \space K = \{ s \}$, the $d(s) = 0$, the assumption is correct.
2. Inductive hypothesis:
   • Suppose the condition is hold when $\vert K \vert = k > 1$.
   • Let $m$ be the latest vertex(the $k$th vertex) added to $K, \space K = \{ s, ..., m \}$.
3. Inductive step:
   • Let $n$ is the next vertex(the $(k+1)$th vertex) that will be added to $K$ (Currently, $n \notin K$).
   • Let $l(m, n)$ be the chosen edge, where $d(n) = d(m) + l(m, n)$. The path from $s$ to $m$ plus $l(m, n)$ denotes $P$, and $Length(P) = d(n)$.
   • Consider another path $\hat{P}$ from $s$ to $n$ via $x$, where $x \ne m$. We will show $Length(\hat{P}) \ge Length(P)$.
   • Let $edge(x, y)$ is the first edge in $\hat{P}$ that leaves $K$. That is, $x \in K$ but $y \notin K$. $\hat{P}$ is one path from $s$ to $x$ to $y$ to $n$.
   • Let $\hat{p}$ be one subpath of $\hat{P}$ from $s$ to $x$, so $Length(\hat{p}) \ge d(x)$
   • $Length(\hat{P}) \ge Length(\hat{p}) + l(x, y)$. ($Length(\hat{P}) = Length(\hat{p}) + l(x, y)$ when $y = n$. In this case, $l(x, n)$ is not chosen, so $Length(\hat{P}) = Length(\hat{p}) + l(x, n) \ge d(m) + l(m, n) = Length(P)$).
   • From above: $Length(\hat{P}) \ge d(x) + l(x, y) \ge d(y)$
   • For all vertices $i \in V - K$ including $y, n$, the minimal $d(i)$ happens when $i = n$, so $d(y) \ge d(n)$. (That's why $n$ is chosen instead of $y$.)
   • Thus, $Length(\hat{P}) \ge d(n) = Length(P)$.

References

• http://www.math.ucsd.edu/~fan/teach/202/notes/04greed.pdf
• https://web.engr.oregonstate.edu/~glencora/wiki/uploads/dijkstra-proof.pdf
• http://web.cs.ucdavis.edu/~amenta/w10/dijkstra.pdf
• http://www.csee.wvu.edu/~ksmani/courses/fa05/gaoa/qen/dijk.pdf